Należy rozwiązać cztery zadania w ciągu 120 minut.

1. Sprowadź do najprostrzej postaci wyrażenie:
   
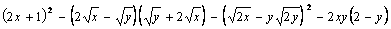
   a następnie oblicz jego wartość dla x=sin30° o y=tg60°.

2. O funkcji f wiadomo, że:
   - jej dziedziną jest zbiór liczb całkowitych,
   - jej wykres jest symetryczny względem osi OY,
   - każdej liczbie całkowietej nieujemnej przyporządkowuje liczbę o b od niej mniejszą, gdzie b jest liczbą, której 15% stanowi wartość wyrażenia:
   
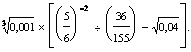
   Narysuj wykres funkcji f. Określ jej miejsce zerowe i zbiory argumentów, dla których jej wartości są dodatnie albo ujemne.

3. Adam i Bartek mieszkają na wsi. Pewnego razu postanowili iść pieszo do pobliskiego miasta. Adam w ciągu połowy czasy, który zużył na dojście do miasta, szedł z prędkością V₁ km/H, a przez resztę czasu - z prędkością V₂ km/h. Bartek połowę drogi ze wsi do miasta szedł z prędkością V₁ km/h, a resztę drogi - z prędkością V₂ km/h. Który z nich dotarł do miasta wcześniej?

4. W trójkącie prostokątnym tangens jednego z kątów ostrych jest równy 0,75, a przeciwprostokątna jest o 4cm dłuższa od dłuższej przyprostokątnej. Oblicz pole koła wpisanego w ten trójkąt.